The black holes of nature are the most perfect macroscopic objects there are in the universe: the only elements in their construction are our concepts of space and time. And since the general theory of relativity provides only a single unique family of solutions for their descriptions, they are the simplest objects as well.
-S. Chandrasekhar, “The Mathematical Theory of Black Holes”, 1983
A binary consisting of two black holes orbiting each other is arguably the simplest macroscopic dynamical system that can be found in Nature. However, despite its minimalist elegance the so-called relativistic two-body problem describing their dynamics, cannot be solved in closed form.
To make progress, we have to introduce some form of approximation scheme. One can discretize the spacetime and solve the Einstein equations on a grid numerically, as is done in Numerical Relativity. This is a highly successful approach, but comes at a (computational) price. A simulation of a that last few tens of orbital cycles before merger can take months of supercomputer time.
Another approach is to study dynamics in the limit where the binary is still very far apart, such that the gravitational interaction is weak, and the motion non-relativistic. In this approach relativistic effects are added order-by-order in the separation as correction to the well known Newtonian two-body problem. This post-Newtonian expansion, was pioneered in the early days of general relativity by Einstein, Lorentz, and Droste, and closed-form analytical results are now available at 4th post-Newtonian order. However, the resulting post-Newtonian expansion is known to only converge as an asymptotic series; at small separations the series diverges, making it unsuitable to study two-body dynamics is the strong field regime.

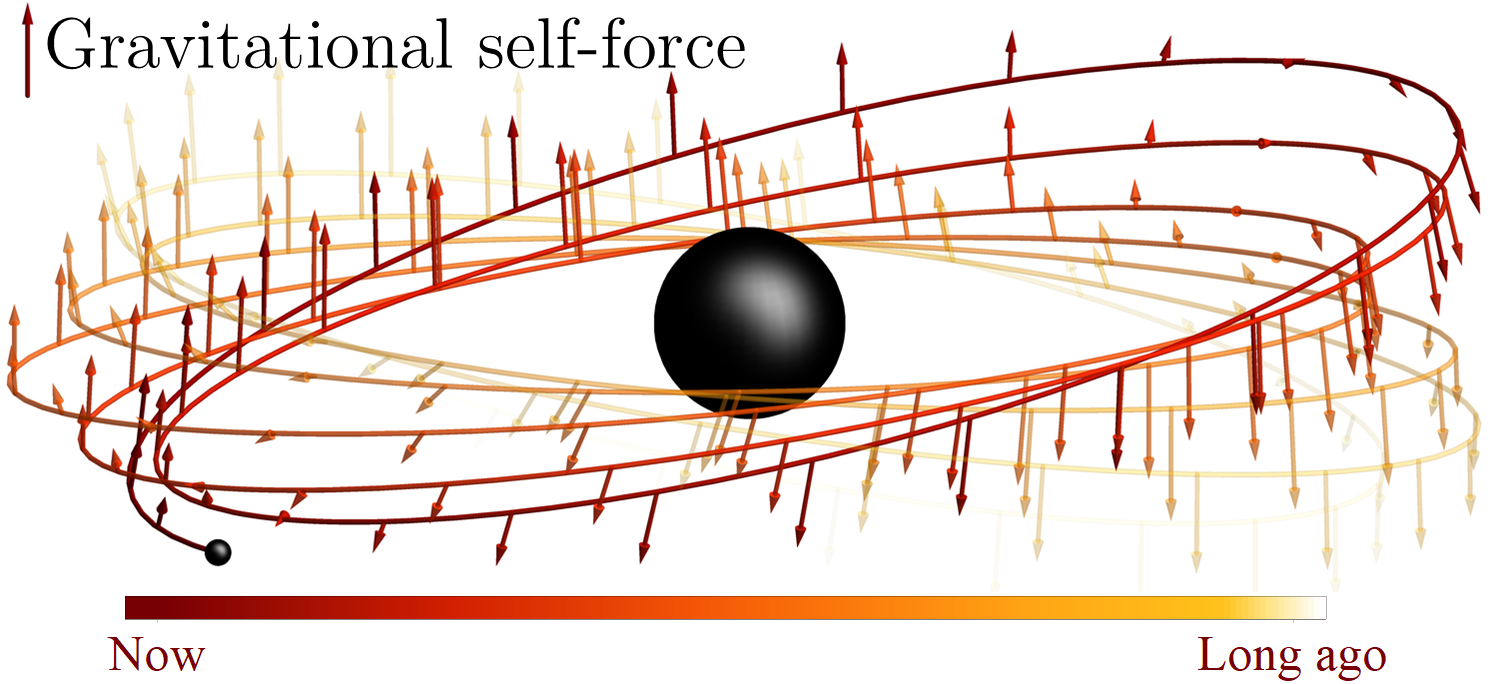
My research focuses primarily on a third approximation scheme, small mass-ratio perturbation theory. In this scheme the dynamics of black hole binaries is systematically expanded in powers of the ratio of their masses. At lowest order, the lighter black hole acts as a test mass following a geodesic in the spacetime generated by the larger black hole. At higher orders, the equations of motion for the smaller object get corrected by an effective force due its own gravitational field, the gravitational self-force.
Development of small mass-ratio perturbation theory requires an elegant combination of analytic and numerical techniques. At leading (geodesic) order, all solutions can be obtained in closed analytic form using elliptic functions. Higher orders require solving the perturbed Einstein equations. Unfortunately, no closed form solutions are available. However, through the use of multi-scale analysis, the non-linear PDEs of the Einstein field equations can reduced to series of uncoupled linear ODEs, which can be solved efficiently to very high precision. Alternatively, one can obtain analytical results by imposing an additional weak-field approximation, resulting in very high-order post-Newtonian results.
One of the interesting aspects of small mass-ratio perturbation theory is that is valid all the way from the weak field regime to the merger in the strong field regime. This means it has the potential to follow the full evolution of a single binary entirely from first principles. This makes it unique among the different approaches to solving the two body problem. The accuracy of the obtained solutions at any given order, is determined solely by the mass-ratio, with mounting evidence that even at low orders in the mass-ratio, small mass-ratio perturbation theory can provide suprisingly accurate results even at equal masses.
Extreme Mass-Ratio Inspirals
Extreme mass-ratio inspirals (EMRIs) are binary systems consisting of a stellar mass compact object (i.e. black hole, neutron star, or white dwarf) orbit a supermassive black hole in the center of a distant galaxy. As the smaller object orbits the supermassive black hole gravitational waves are created causing the orbit to shrink until the small object drops into the supermassive black hole.
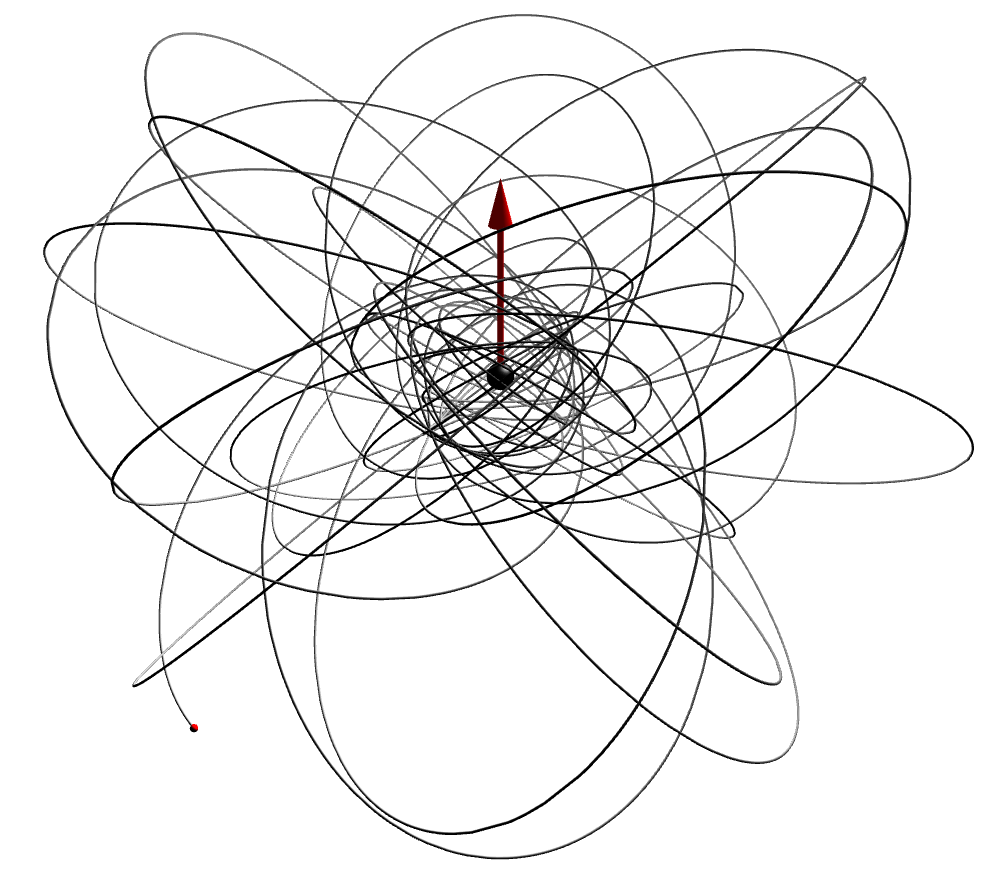
What makes EMRIs interesting is that the amount that a binary shrinks per orbit is proportional to the ratio of the masses of the two object. The extremely small mass-ratio of an EMRI thus implies that EMRIs spend a very large number of orbits in the last stage of the inspiral where the gravitational fields are strong. In the process it weaves an intricate map of the space-time around the supermassive black hole into the gravitational wave signal.
The space based gravitational wave observatory LISA (planned for launch in 2034) will be able to detect the gravitational waves from such events. It is note quite known how many EMRIs should be observable, but our best estimates range from 10s to 100s per year.
When observed we can infer properties of the EMRI and the surrounding spacetime by comparing the signal with theoretically predicted templates. In the process, we will get extra-ordinairily accurate measurements of the various properties (such as masses and spins) of the EMRI, and will be able to probe for deviation from the general relativity prediction that could hint at new physics.
The defining feature of EMRIs is of course their extremely small (typically around 10-5) mass-ratios. Small mass-ratio perturbation theory is the only approach to modelling binaries that can handle this regime, and is therefore an essential ingredient for learning anything from EMRIs. To obtain waveforms that stay in phase over an inspiral timescale, requires both the first and second order gravitational self-force. In most situations this will also be sufficient.
Ongoing research interests
- Developing GSF/SMR theory
- Practical calculations of second order GSF on spinning binaries
- New/improved methods for obtaining first order GSF
- Development of efficient SMR based waveform models for LISA
- Interfaces between different approaches to waveform modelling
- Effects in EMRIs due to orbital resonances
- Excitation of QNMs during the inspiral phase.